Fixed Point Computation

Introducing fixed point for efficiency, predictability and low cost, which are essential in many real-time and embedded DSP applications.

Table of Contents

1. Fundamentals
2. Arithmetic
3. Precision
4. Overflow
5. Compare to Floating Point
6. Demo

1. Fundamentals

Fixed-point representation is a way to represent real numbers (i.e., numbers with fractions/decimals) using integers, by fixing the position of the binary point (similar to the decimal point, but in binary).

Representation

Fixed point numbers are typically represented as Qm.n where:

• $m$ is the number of integer bits
• $n$ is the number of fractional bits.

For example, Q1.15 means 1 integer bit(signed bit), 15 fractional bits. Other common formats include Q1.31, Q8.8, Q16.16 etc.

Conversion

Assume the fixed point format is Qm.n, to convert a real number(R) to a fixed point(F):
$$
\begin{equation}
F = R \times 2^{n}
\end{equation}
$$

to convert a fixed point(F) to a real number(R):
$$
\begin{equation}
R = \frac{F}{2^{n}}
\end{equation}
$$

To demonstrate this, let’s use format Q1.3 (1 bit for sign bit, 3 bits for fractional part) as an example.

Let’s try 0101:

• Sign bit is 0 -> it’s positive
• Binary 0101 = decimal 5
• Convert to real number:
  $$
  \begin{equation}
  \frac{5}{2^{3}} = 0.625
  \end{equation}
  $$

So, 0101 in Q1.3 = 0.625

What if it is negative? Let’s try binary 1101.

• The MSB is 1, so it is a negative.
• Take the two’s complement to find the magnitude and add 1: 1101 -> 0010 -> 0011.
• Convert 0011 to decimal: 3.
• Add the sign back: -3
• Convert to real number:
  $$
  \begin{equation}
  \frac{-3}{2^{3}} = -0.375
  \end{equation}
  $$

Two’s Complement

Since we used two’s complement above, it is worth mentioning about what it is and why it is useful. It is a special representation of signed integers that can make addition, subtraction, and other arithmetic to work correctly for both positive and negative numbers.

For Q1.2, all the possible values from min to max.

Binary	Signed Int	Real Value (= int / 4)
100	−4	−1.00
101	−3	−0.75
110	−2	−0.50
111	−1	−0.25
000	0	0.00
001	1	0.25
010	2	0.50
011	3	0.75

Each step = $\frac{1}{2^2} = 0.25$

Range(minimum & maximum)

From the table above, we can easily find the pattern that, for a Qm.n format fixed point.

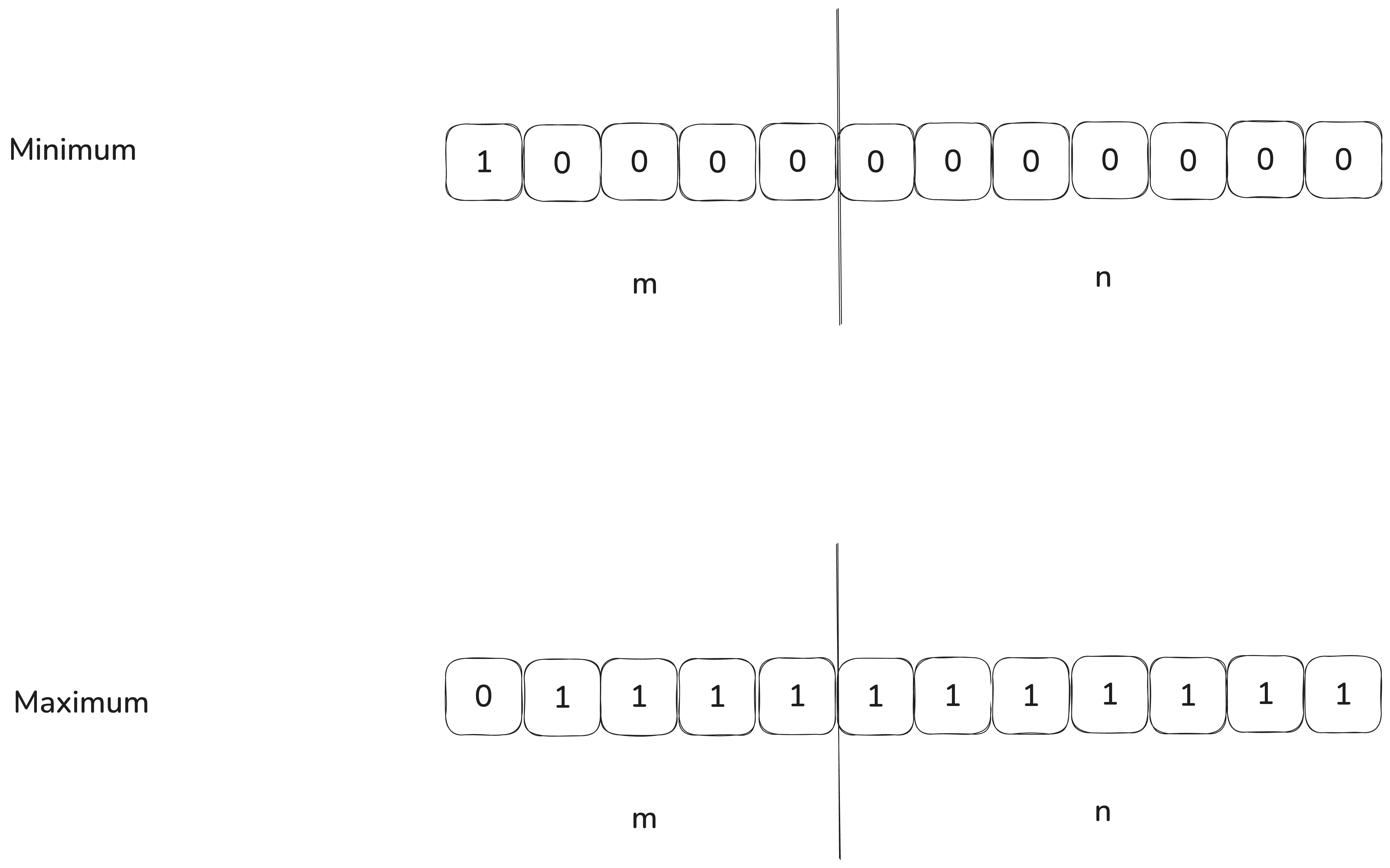
Therefore, for minimum (invert and add 1):
$$
\begin{equation}
\frac{2^{m+n-1}}{2^{n}} = -2^{m-1}
\end{equation}
$$

For maximum:
$$
\begin{equation}
\frac{2^{m+n-1} - 1}{2^{n}} = 2^{m-1} - 2^{-n}
\end{equation}
$$

2. Arithmetic

Before we dive into the fixed point arithmetic, let’s assume that we are using format: Q4.4.

For Q4.4, its representation range is:

$$
\begin{equation}
min = -2^{m-1} = -\frac{2^7}{2^4} = -8 \\
max = 2^{m-1} - 2^{-n} = 2^3 - 2^{-4} = 7.9375
\end{equation}
$$

Recap: the conversion between fixed point and its floating point value
$$
\begin{equation}
result_{fix} = result_{real} \times 2^{n}
\end{equation}
$$

Addition
$$
\begin{equation}
a_{real} = \frac{a_{fix}}{2^n} \\
b_{real} = \frac{b_{fix}}{2^n} \\
a + b = \frac{a_{fix}+b_{fix}}{2^n}
\end{equation}
$$

If we want to add 2.5 and 1.25.

$$
\begin{equation}
a_{fix} = 2.5 \times 2^{4} = 40 \\
b_{fix} = 1.25 \times 2^{4} = 20 \\
\\
result_{fix} = a_{fix} + b_{fix} = 60 \\
result_{real} = \frac{60}{2^{4}} = 3.75, \text{which equals to } 2.5 + 1.25 = 3.75
\end{equation}
$$

Subtraction

Similar to addition
$$
\begin{equation}
a_{real} = \frac{a_{fix}}{2^n} \\
b_{real} = \frac{b_{fix}}{2^n} \\
a - b = \frac{a_{fix}-b_{fix}}{2^n}
\end{equation}
$$

$$
\begin{equation}
a_{fix} = 2.5 \times 2^{4} = 40 \\
b_{fix} = 1.25 \times 2^{4} = 20 \\
\\
result_{fix} = a_{fix} - b_{fix} = 20 \\
result_{real} = \frac{20}{2^{4}} = 1.25, \text{which equals to } 2.5 - 1.25 = 1.25
\end{equation}
$$

Multiplication

Integer multiplication will cause overflow, for example, $6 \times 5 = 30$, 30 exceeds the maximum value Q4.4 can represent. Therefore, for multiplication, we need to scale down the value. The rule is:
$$
\begin{equation}
result_{fix} = \frac{a_{fix} \times b_{fix}}{2^n}
\end{equation}
$$

Example: $2.5 \times 1.5$

$$
\begin{equation}
a_{fix} = 2.5 \times 2^{4} = 40 \\
b_{fix} = 1.5 \times 2^{4} = 24 \\
\\
result_{fix} = a_{fix} \times b_{fix} = 960 \\
result_{scaled} = \frac{960}{2^4} = 60 \\
result_{real} = \frac{60}{2^4} = 3.75
\end{equation}
$$

Devision

To divide without losing precision, upscale numerator before division:
$$
\begin{equation}
result_{fix} = \frac{a_{fix} \times 2^{n}}{b_{fix}}
\end{equation}
$$

Example: $2.5 \div 1.25$

$$
\begin{equation}
a_{fix} = 2.5 \times 2^{4} = 40 \\
b_{fix} = 1.25 \times 2^{4} = 20 \\
\\
a_{fix-upscaled} = 40 \times 2^{4} = 640 \\
result_{fix} = \frac{640}{20} = 32 \\
result_{real} = \frac{32}{2^4} = 2
\end{equation}
$$

3. Precision

Qm.n

We use the term “resolution” to represent the smallest step(or precision step) of a fixed point format.
$$
\begin{equation}
\text{resolution} = \frac{1}{2^n}
\end{equation}
$$

For example:

• Q1.7 has resolution of $\frac{1}{2^7} = 0.0078125$
• Q4.4 has resolution of $\frac{1}{2^4} = 0.0.0625$

More fractional bits mean better precision, but smaller range(suppose we have fixed total bits).

Truncation error

Example: convert 0.1 to Q4.4 fixed point
$$
\begin{equation}
result_{fix} = 0.1 \times 2^{4} = 1.6 \\
\text{Truncation discards fractional bits without rounding: } result_{trunc} = floor(1.6) = 1 \\
result_{real} = \frac{1}{2^4} = 0.0625 \neq 0.1
\end{equation}
$$

Rounding error

Same example: convert 0.1 to Q4.4 fixed point
$$
\begin{equation}
result_{fix} = 0.1 \times 2^{4} = 1.6 \\
\text{Rounding to nearest is better, but still introduces error: } result_{round} = round(1.6) = 2 \\
result_{real} = \frac{2}{2^4} = 0.125 \neq 0.1
\end{equation}
$$

Compare the two results above:
$$
\begin{equation}
\text{rounding_error} = |0.125 - 0.1| = 0.025 \\
\text{truncation_error} = |0.0625 - 0.1| = 0.0375
\end{equation}
$$

Rounding to the nearest can be a better strategy to reduce precision loss. There is one trick which is to add a rounding offset before scaling.
$$
\begin{equation}
result_{fix} = ((a_{fix} \times b_{fix}) + (1 \ll (n - 1))) \gg n
\end{equation}
$$

For example, in fixed point multiplication, $0.5 \times 0.3 = 0.15$

Without rounding:
$$
\begin{equation}
a_{fix} = 0.5 \times 2^4 = 8 \\
b_{fix} = 0.3 \times 2^4 = round(4.8) = 5 \\
result_{fix} = (8 \times 5) \gg 4 = 2 \text{truncated}\\
result_{real} = \frac{2}{2^4} = 0.125 \\
\text{error: } 0.125 - 0.15 = -0.025
\end{equation}
$$

With rounding:
$$
\begin{equation}
a_{fix} = 0.5 \times 2^4 = 8 \\
b_{fix} = 0.3 \times 2^4 = round(4.8) = 5 \\
result_{fix-rounding} = ((a_{fix} \times b_{fix}) + (1 \ll (n - 1))) \gg n = (8 \times 5 + (1 \ll 3)) \gg 4 = (40 + 8) \gg 4 = 3 \\
result_{real} = \frac{3}{2^4} = 0.1875 \\
\text{error: } |0.1875 - 0.15| = 0.0375
\end{equation}
$$

At first glance, +0.0375 seems worse than −0.025, because it’s a larger absolute error. So why do we still say that rounding is better?

The reason rounding is preferred is not always because it produces the smallest possible error for each operation — but because it produces statistically unbiased results on average across many operations.

Truncation always drops the fractional part, rounding down toward zero. This introduces a consistent negative bias. Over many computations:

1. You might repeatedly lose small bits of precision
2. The result accumulates a consistent downward error
3. This is called systematic error

Rounding to nearest:

1. Sometimes you round up
2. Sometimes you round down
3. On average, the errors cancel out

This leads to a smaller total error over time and more accurate aggregate results.

4. Overflow

In fixed-point systems, overflow occurs when the result of an operation exceeds the representable range of the format (e.g., Q4.4 can represent only from −8.0 to +7.9375).

Let’s use fixed point multiplication as an example. If we are calculating $3.5(a) \times 1.5(b)$, the fixed point representations for $a$ and $b$ are:
$$
\begin{equation}
a_{fix} = 3.5 * 2^4 = 56 \\
b_{fix} = 1.5 * 2^4 = 24
\end{equation}
$$

Then, the multiplication result is:
$$
\begin{equation}
56 * 24 = 1344
\end{equation}
$$

Since $1344$ exceeds the maximum(127) of 8-bit signed integer, if we still use int8 data type to catch the result, we will get:

• 1344 in binary: 0000 0101 0100 0000 (16-bit)
• The lower 8 bits are 01000000, which equals 64 in decimal.

The final result(after we convert it to the floating point representation) will be:
$$
\begin{equation}
result_{real} = \frac{64}{2^4} = 4 \neq (3.5 * 1.5 = 5.25)
\end{equation}
$$

The most common techniques we use to handle arithmetic overflow is to use wider intermediate types. We use 16-bit for 8-bit math. Let’s redo the math for the multiplication above.

$$
\begin{equation}
a_{fix} = 3.5 * 2^4 = 56 \\
b_{fix} = 1.5 * 2^4 = 24 \\
a_{fix} * b_{fix} = 1344 \text{ (use 16-bit to hold the result)} \\
result_{fix} = (1344 + 2^{3}) / 2^{4} = 84 \text{ (add rounding offset)} \\
result_{real} = \frac{84}{2^4} = 5.25 = 3.5 * 1.5
\end{equation}
$$

Clamping
Sometimes, even if we use wider intermediate types, after we scale the result down to the smaller range, it is still out of the range. This is when we need clamping to ensure the final result is within the range.

For multiplication $7.5 \times 1.5$ using Q4.4 format:

$$
\begin{equation}
a_{fix} = 7.5 * 2^4 = 120 \\
b_{fix} = 1.5 * 2^4 = 24 \\
a_{fix} * b_{fix} = 2880 \text{ (use 16-bit to hold the result)} \\
result_{fix} = (2880 + 2^{3}) / 2^{4} = 180 \text{ (add rounding offset)} \\
\end{equation}
$$

The valid range for Q4.4 is: $-128$ to $127$. Obviously, $180$ exceeds $127$. We need to clamp to maximum Q4.4 value:
$$
\begin{equation}
result_{fix} = min(180, 127) = 127 \\
result_{real} = \frac{127}{2^4} = 7.9375 \neq (7.5 * 1.5 = 11.25) \text{ precision loss}
\end{equation}
$$

The code example below demonstrates the Q4.4 multiplication process.

int8_t fixed_mul_q4_4(int8_t a, int8_t b) {
    int16_t temp = (int16_t)a * (int16_t)b;      // intermediate is wider
    temp = (temp + 8) >> 4;                      // rounding
    if (temp > 127) temp = 127;                  // clmap/saturation
    if (temp < -128) temp = -128;
    return (int8_t)temp;
}

5. Compare to Floating Point

We have beeing talking so much about the basics of fixed point computation, but so far, we haven’t touched the most important part, which is why we prefer fixed point arithmetic over floating point, especially in embedded systems, DSP, mobile devices, or hardware where performance, power, and cost matter.

You might wonder about an alternative approach: why not simply use FP16 instead of FP32 for floating-point operations? This would allow us to match the bit width of typical fixed point implementations (16 bits) while retaining floating-point capabilities. But are they really the same? To answer this question, we need to understand how fixed point and floating point work differently at a low level perspective.

Floating point
IEEE 754 Half-Precision

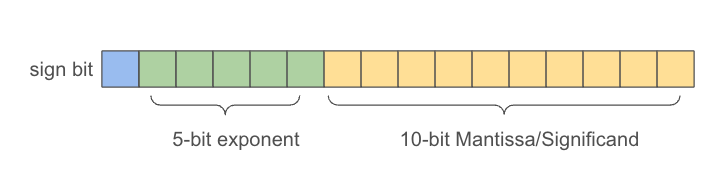
$$
(-1)^{sign} \times (1 + mantissa) \times 2^{exponent-15}
$$

Floating point arithmetic(addition) by steps from low level perspective

Step	Description
1. Unpack	Extract sign, exponent, mantissa
2. Align exponents	Shift smaller mantissa to match the larger exponent
3. Add mantissas	Perform integer addition of aligned mantissas
4. Normalize	Shift result to maintain 1.xxx format, adjust exponent accordingly
5. Round	Round result to fit in mantissa bits
6. Repack	Combine sign, new exponent, and rounded mantissa into 16-bit float format

Fixed point

As we discussed in section 2, fixed point arithmetics are just simple integer operations as long as both numbers are in the same format (Qm.n). Compared to floating point, there is no extra alignment, rounding, normalizing, and handling special cases. Less CPU cycles needed for fixed point operations.

Hardware differences:

1. Fixed point can be implemented on tiny MCUs without an FPU, using only arithmetic logic unit(ALU) — less silicon, less power, less cost.
2. Floating point requires dedicated hardware(FPU) or software emulation — more cycles, more power, larger chip.

6. Demo

Converting a Gaussian blur implementation from floating point to fixed point

Floating Point Gaussian Blur (1D)

void gaussianBlurFloat(const float* input, float* output, int size) {
    const float kernel[5] = { 0.0625, 0.25, 0.375, 0.25, 0.0625 };

    for (int i = 2; i < size - 2; ++i) {
        output[i] = 0.0f;
        for (int j = -2; j <= 2; ++j) {
            output[i] += input[i + j] * kernel[j + 2];
        }
    }
}

Choose a Fixed Point Format
Assume:

1. Input & output are in int16_t using Q8.8 format (8 integer bits, 8 fractional bits).
2. We’ll convert kernel coefficients to Q1.15 format (pure fractional, for more precision).
3. Multiply Q8.8 × Q1.15 → result is Q9.23 → shift by 15 bits to get back to Q8.8.

Convert Kernel to Fixed Point

// Multiply each float coefficient by 2^15 = 32768
const int16_t kernel[5] = {
    0.0625  * 32768,  // ≈ 2048
    0.25    * 32768,  // ≈ 8192
    0.375   * 32768,  // ≈ 12288
    0.25    * 32768,  // ≈ 8192
    0.0625  * 32768   // ≈ 2048
};

Implementation Details

void gaussianBlurFixed(const int16_t* input, int16_t* output, int size) {
    const int16_t kernel[5] = { 2048, 8192, 12288, 8192, 2048 }; // Q1.15

    for (int i = 2; i < size - 2; ++i) {
        int32_t acc = 0;
        for (int j = -2; j <= 2; ++j) {
            int32_t sample = (int32_t)input[i + j];        // Q8.8
            int32_t k = (int32_t)kernel[j + 2];             // Q1.15
            acc += (sample * k);                            // Q8.8 × Q1.15 = Q9.23
        }
        // Round and shift to bring Q9.23 → Q8.8
        acc = (acc + (1 << 14)) >> 15;
        
        // Optional: clip to int16_t range
        if (acc > 32767) acc = 32767;
        if (acc < -32768) acc = -32768;

        output[i] = (int16_t)acc;
    }
}