Calculate Projection Matrix

Derive the form of the projection matrix mathematically

1. Understand Eye Coordinate and NDC

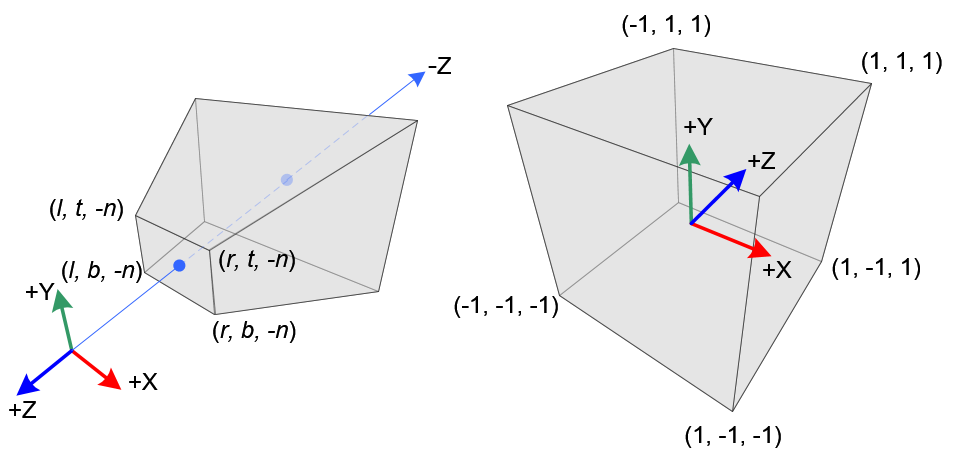
Eye coordinate and normal device coordinate(from: https://www.songho.ca/opengl/gl_projectionmatrix.html)

Camera is looking at the -Z direction in eye coordinate space, but it is looking towards +Z direction in NDC.

2. Some Properties

Projection matrix a 4x4 matrix and what it does is to transform eye coordinates to clip coordinates.

$$
\begin{bmatrix}
x_c \\
y_c \\
z_c \\
w_c \\
\end{bmatrix} =
M_{projection} \times
\begin{bmatrix}
x_e \\
y_e \\
z_e \\
w_e \\
\end{bmatrix}
$$

NDC can be obtained by dividing the clip coordinates by the w component.

$$
\begin{bmatrix}
x_n \\
y_n \\
z_n \\
\end{bmatrix} =
\begin{bmatrix}
\frac{x_c}{w_c} \\
\frac{y_c}{w_c}\\
\frac{z_c}{w_c}\\
\end{bmatrix}
$$

These are all we need to know. Consider these steps as standard routines to convert coordinate in eye space to NDC.

3. Eye Coordinates to Projection Coordinates

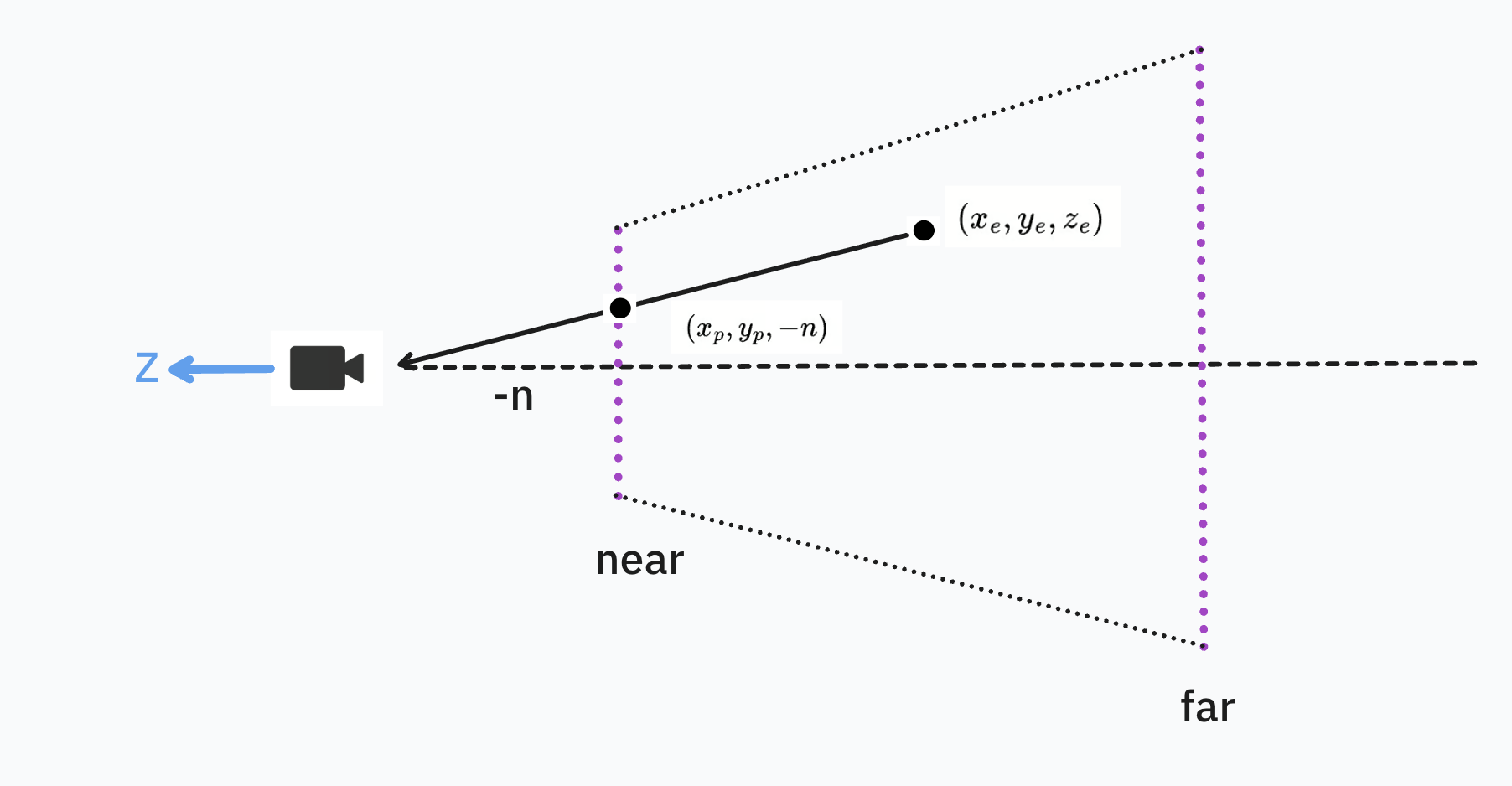
We define projection coordinates as the projection of eye coordinates onto the near plane. Based on the property of similar triangle, we can get:

$$
x_p = \frac{n \times x_e}{-z_e} \\
x_p = \frac{n \times y_e}{-z_e}
$$

4. Projection Coordinates to NDC

It is a linear mapping.

• For $x_p$ to $x_n$, it is $[left, right] \Rightarrow [-1, 1]$.
• For $y_p$ to $y_n$, it is $[bottom, top] \Rightarrow [-1, 1]$.

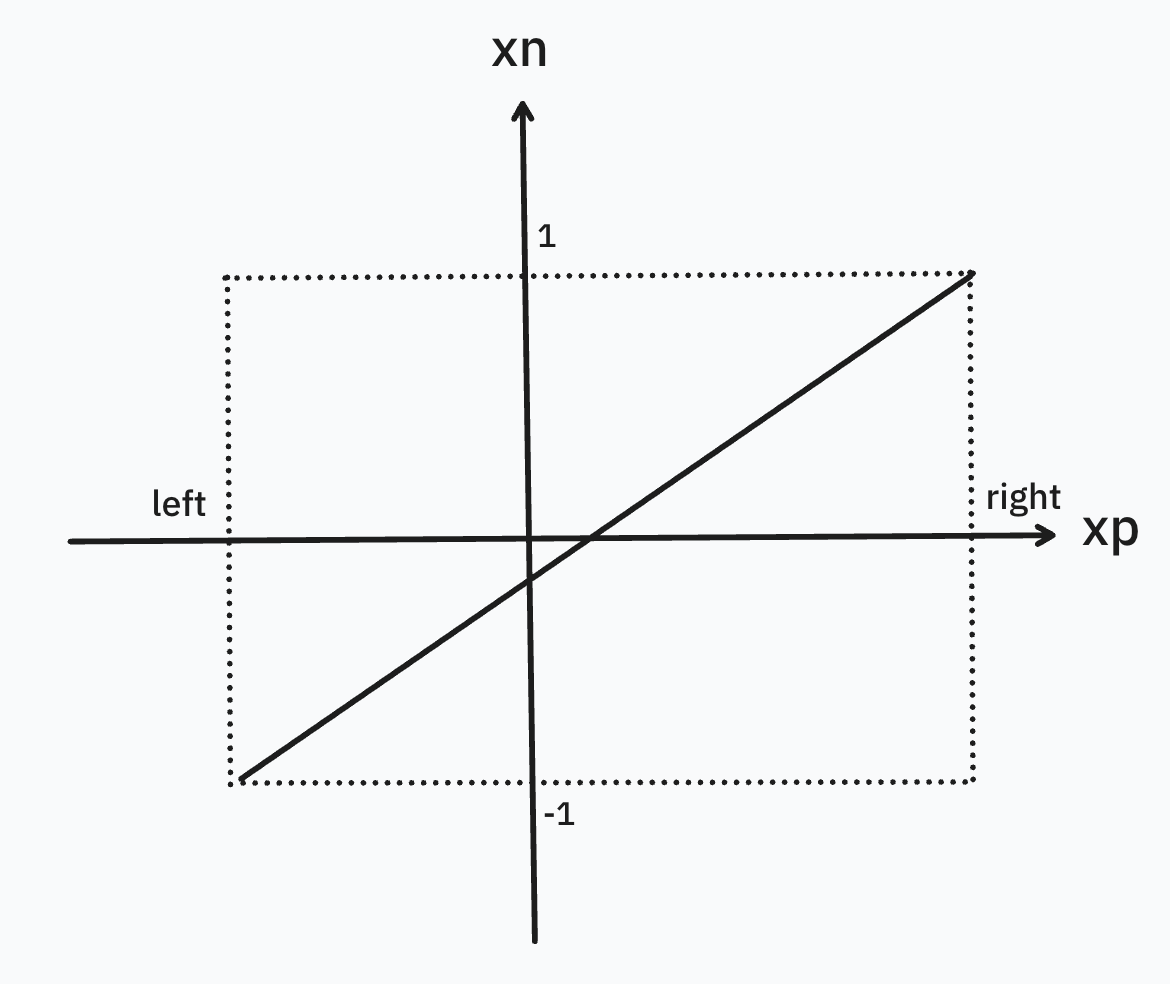
$$
x_n = ax_p + b;
$$

We have:
$$
a = \frac{2}{r - l} \\
1 = ar + b \\
$$

Substitute $a$:
$$
1 = \frac{2}{r - l} \times r + b \\
$$

So,
$$
b = \frac{r - l - 2r}{r - l} = \frac{-r - l}{r - l} = -\frac{r + l}{r - l}
$$

Overall,
$$
x_n = \frac{2}{r - l}x_p - \frac{r + l}{r - l}
$$

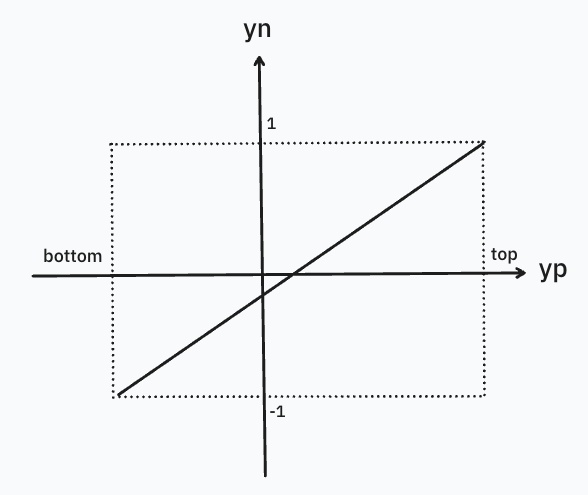
Similarly, we can follow the exact same steps to get the relation of $y_n$ and $y_p$

$$
y_n = \frac{2}{t - b}y_p - \frac{t + b}{t - b}
$$

5. Eye Coordinates to NDC

Since we already know how to do the conversions:

1. From eye coordinates to projection coordinates.
2. From projection coordinates to NDC.

It is easy to obtain the conversion from: eye coordinates to NDC.

\begin{cases}
x_p = \frac{nx_e}{-z_e} \\
x_n = \frac{2}{r - l}x_p - \frac{r + l}{r - l}
\end{cases}

Substitute $x_p$ into the second equation. We can get:

$$
x_n = \frac{\frac{2n}{r - l}x_e + \frac{r + l}{r - l}z_e}{-z_e}
$$

Let’s recall the projection matrix:

$$
\begin{bmatrix}
x_c \\
y_c \\
z_c \\
w_c \\
\end{bmatrix} =
M_{projection} \times
\begin{bmatrix}
x_e \\
y_e \\
z_e \\
w_e \\
\end{bmatrix}
$$

If i am telling you $w_c = -z_e$, does it make sense to you?

Because $x_n$ will eventually get calcualted as $\frac{x_c}{w_c}$, the equation we got above fits this form perfectly.

\begin{cases}
x_n = \frac{x_c}{w_c} \\
x_n = \frac{\frac{2n}{r - l}x_e + \frac{r + l}{r - l}z_e}{-z_e}
\end{cases}

We can write the projection matrix partially as:

$$
\begin{align}
\begin{bmatrix}
x_c \\
y_c \\
z_c \\
w_c \\
\end{bmatrix}
&=
\begin{bmatrix}
\frac{2n}{r-l} & 0 & \frac{r + l}{r - l} & 0 \\
. & . & . & . \\
. & . & . & . \\
0 & 0 & -1 & 0
\end{bmatrix}
\begin{bmatrix}
x_e \\
y_e \\
z_e \\
w_e \\
\end{bmatrix}
\end{align}
$$

Following the same steps above, we can get the relation between $y_n$ and $y_e$

$$
y_n = \frac{\frac{2n}{t - b}y_e + \frac{t + b}{t - b}z_e}{-z_e}
$$

Now, the projection matrix becomes:

$$
\begin{align}
\begin{bmatrix}
x_c \\
y_c \\
z_c \\
w_c \\
\end{bmatrix}
&=
\begin{bmatrix}
\frac{2n}{r-l} & 0 & \frac{r + l}{r - l} & 0 \\
0 & \frac{2n}{t-b} & \frac{t + b}{r - b} & 0 \\
. & . & . & . \\
0 & 0 & -1 & 0
\end{bmatrix}
\begin{bmatrix}
x_e \\
y_e \\
z_e \\
w_e \\
\end{bmatrix}
\end{align}
$$

6. Find $z_n$

What’s missing right now is the third row. And we are pretty sure that $z_n$ has nothing to do with both $x_e$ and $y_e$. So, to rewrite the projection matrix again:

$$
\begin{align}
\begin{bmatrix}
x_c \\
y_c \\
z_c \\
w_c \\
\end{bmatrix}
&=
\begin{bmatrix}
\frac{2n}{r-l} & 0 & \frac{r + l}{r - l} & 0 \\
0 & \frac{2n}{t-b} & \frac{t + b}{r - b} & 0 \\
0 & 0 & A & B \\
0 & 0 & -1 & 0
\end{bmatrix}
\begin{bmatrix}
x_e \\
y_e \\
z_e \\
w_e \\
\end{bmatrix}
\end{align}
$$

We have $z_n$ as:

$$
z_n = \frac{Az_e + Bw_e}{-z_e}
$$

In eye coordinates, $w_e = 1$

$$
z_n = \frac{Az_e + B}{-z_e}
$$

Solving for $A$ and $B$ is easy because we know that $z_e = -n$ maps to $z_n = -1$, and $z_e = -f$ maps to $z_n = 1$.

\begin{cases}
-1 = \frac{-An + B}{n} \\
1 = \frac{-Af + B}{f}
\end{cases}

Then,
\begin{cases}
A = -\frac{f + n}{f - n} \\
B = -\frac{2fn}{f - n}
\end{cases}

Now, we can finally complete the projection matrix.

$$
\begin{align}
\begin{bmatrix}
x_c \\
y_c \\
z_c \\
w_c \\
\end{bmatrix}
&=
\begin{bmatrix}
\frac{2n}{r-l} & 0 & \frac{r + l}{r - l} & 0 \\
0 & \frac{2n}{t-b} & \frac{t + b}{r - b} & 0 \\
0 & 0 & -\frac{f + n}{f - n} & -\frac{2fn}{f - n} \\
0 & 0 & -1 & 0
\end{bmatrix}
\begin{bmatrix}
x_e \\
y_e \\
z_e \\
w_e \\
\end{bmatrix}
\end{align}
$$

7. Simplied Form

Normally, the frustum is symmetric, so we have:

$$
\begin{cases}
r + l = 0 \\
t + b = 0 \\
r - l = w \\
t - b = h
\end{cases}
$$

Where $w$ is the width, and $h$ is the height.

The projection matrix becomes:
$$
\begin{align}
\begin{bmatrix}
x_c \\
y_c \\
z_c \\
w_c \\
\end{bmatrix}
&=
\begin{bmatrix}
\frac{2n}{w} & 0 & 0 & 0 \\
0 & \frac{2n}{h} & 0 & 0 \\
0 & 0 & -\frac{f + n}{f - n} & -\frac{2fn}{f - n} \\
0 & 0 & -1 & 0
\end{bmatrix}
\begin{bmatrix}
x_e \\
y_e \\
z_e \\
w_e \\
\end{bmatrix}
\end{align}
$$

8. Projection Matrix With FOV

In glm::perspective(), we often provide the window aspect ratio to compute the projection matrix.

glm::mat4 projection = glm::perspective(glm::radians(45.0f), static_cast<float>(kWidth) / static_cast<float>(kHeight), 0.1f, 100.0f);

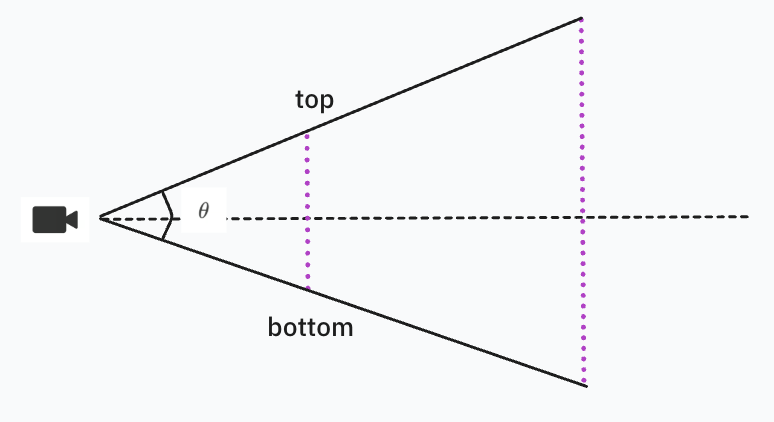
$$
\begin{cases}
\tan(\frac{\theta}{2}) = \frac{t}{n} \\
\frac{r}{t} = \frac{w}{h}
\end{cases}
$$

By specifying the $\theta$ values for vertical and horizontal, we can either get $t$ or $r$. Then the other one can be obtained using the window aspect ratio $\frac{w}{h}$.

References

• https://www.songho.ca/opengl/gl_projectionmatrix.html