Camera Intrinsic and Extrinsic

Deriving the Camera Intrinsic and Extrinsic Matrices.

1. Introduction

Commonly Used Coordinate Systems

• World Coordinate System
• Camera Coordinate System
• Image Coordinate System
• Pixel Coordinate System

Camera intrisics and extrinsics describe the transformation from one coordinate system to another.

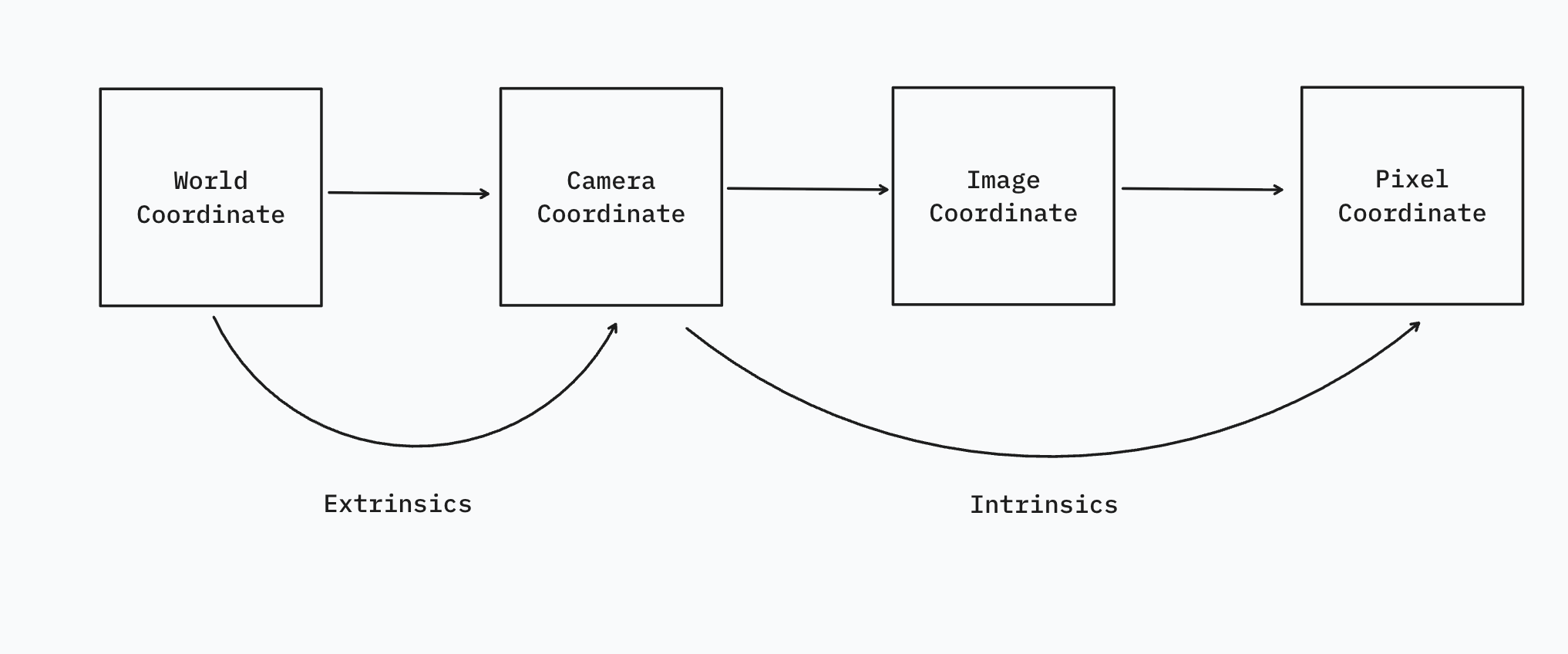
2. Camera Extrinsics

World to Camera
If we define a point in the world coordinate system as:

$$
P_w=(X_w, Y_w, Z_w)
$$

And the same point but in camera coordiante system:

$$
P_c=(X_c, Y_c, Z_c)
$$

From World coordinate to Camera coordinate, the transformation is simply translation(T) + rotation(R). It can be represented as a transformation matrix.

$$
\begin{bmatrix}
X_c \\
Y_c \\
Z_c
\end{bmatrix} =
\begin{bmatrix}
R_{3\times 3} & T_{3\times 1}
\end{bmatrix}
\begin{bmatrix}
X_w \\
Y_w \\
Z_w \\
1
\end{bmatrix}
$$

$\begin{bmatrix}R & T\end{bmatrix}$ is the Camera Extrinsic Matrix.

3. Camera Intrinsics

3.1 Camera to Image

Image is a 2D plane and the image coordinate $P_i(X_i, Y_i)$ is the projection of $P_c(X_c, Y_c, Z_c)$ onto this 2D plane.

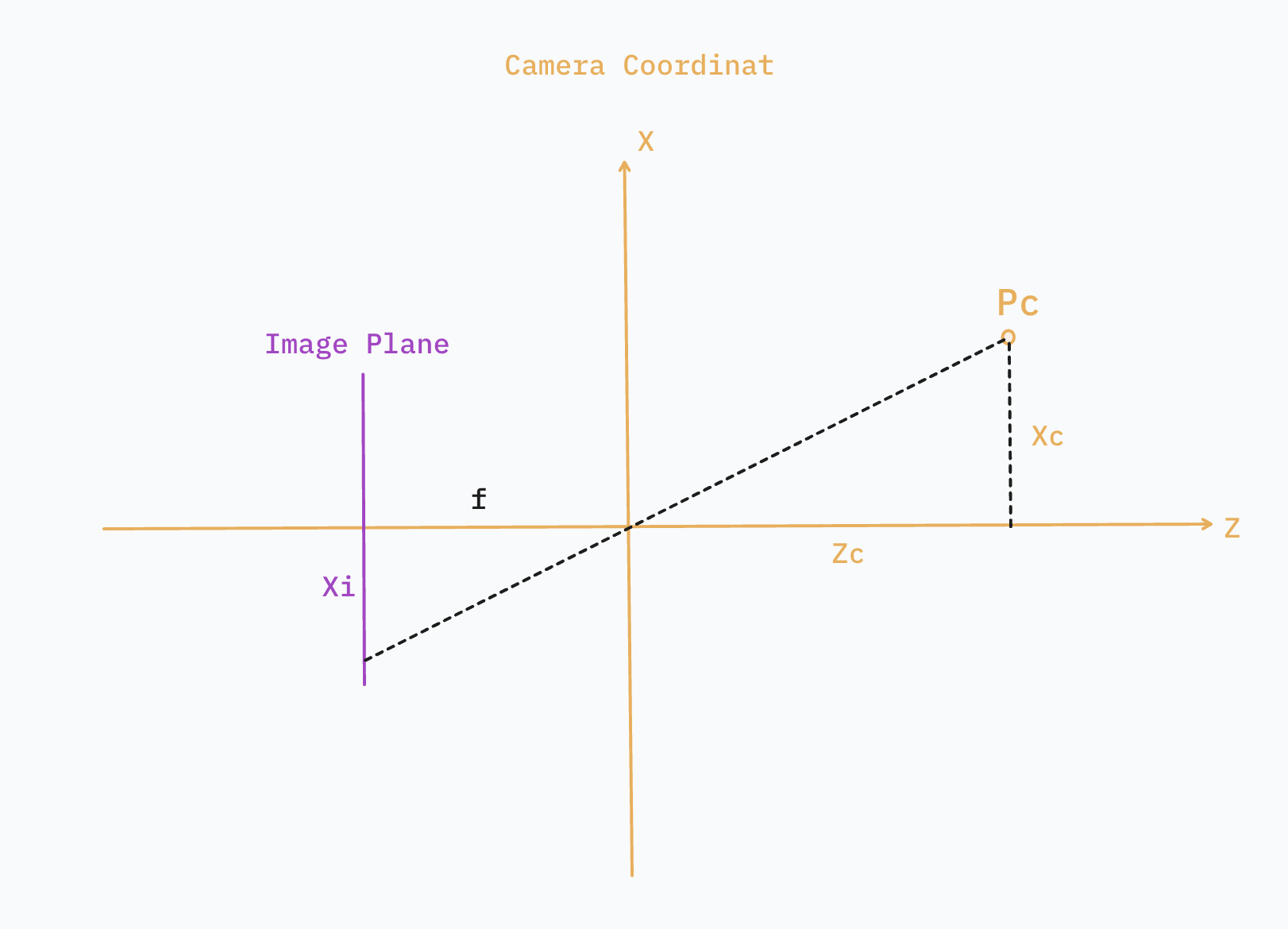
In the pinhole camera model, we place the image plane one focal length ($f$) away from the camera center, making it straightforward to compute how a 3D point($P_c$ in Camera Coordinate) projects onto the image plane.

In real cameras, though, light passes through a thin lens, bending according to lens refraction rather than traveling straight through a pinhole. So why do we still rely on the pinhole model? Let’s first take a look at how light actually travels through a thin lens.

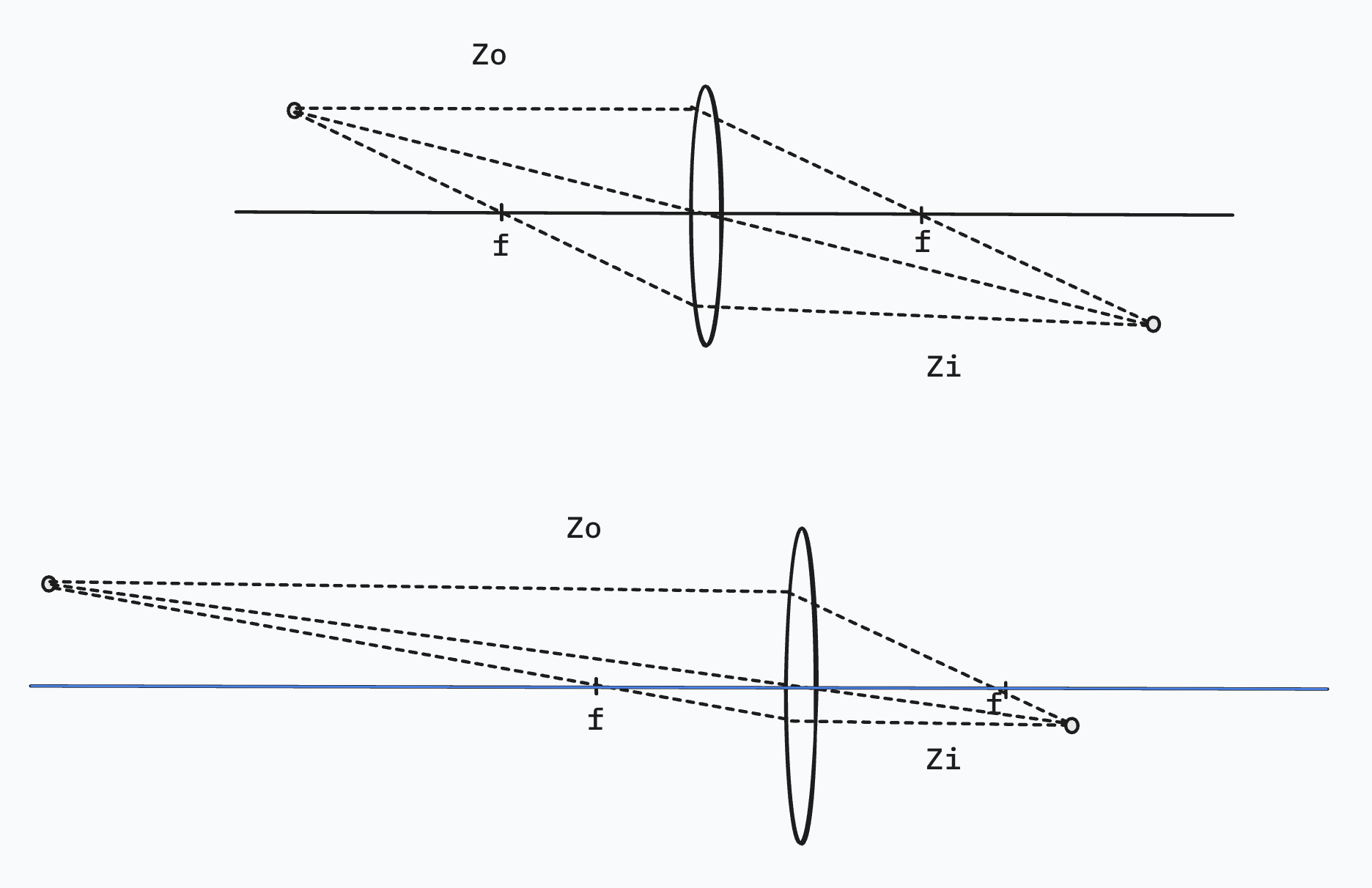
The thin-lens equation states that:

$$
\frac{1}{f} = \frac{1}{Z_{o}} + \frac{1}{Z_i}
$$

Where $f$ is the focal length, $Z_o$ is the object distance to the lens and $Z_i$ is the formed image distance to the lens. As we move the object away from the lens, the image is gettng closer to the focal length distance.

Usually, $Z_o \gg f$, e.g. $Z_o = 1m$ and $f=5mm$,

$$
Z_i = \frac{fZ_o}{Z_o - f} = \frac{1 * 0.005}{1 - 0.005} = 5.025mm
$$

The object projection(image) is only a little bit behind the focal length. Such small errors can be neglected and it is fine use $Z_i = f$ for mathmatical simplicity.

So, based on the property of similar triangles:

$$
\frac{X_c}{Z_c} = \frac{X_i}{f} \\
X_i = f\frac{X_c}{Z_c}
$$

Same for Y-axis:
$$
Y_i = f\frac{Y_c}{Z_c}
$$

We can further simplify the equations above by letting $Z_c = 1$, since $P_i$ is independent of $Z_i$(as long as $P_c$ lies on the same projection ray).

$$
\begin{cases}
X_i = fX_c \\
Y_i = fY_c
\end{cases}
$$

To rewrite it in a matrix form:
$$
\begin{bmatrix}
X_i \\
Y_i \\
1
\end{bmatrix} =
\begin{bmatrix}
f & 0 & 0 \\
0 & f & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
X_c \\
Y_c \\
1 \\
\end{bmatrix}
$$

Focal lengths of $XY$ axises are not always identical, so its representation can be:
$$
\begin{bmatrix}
X_i \\
Y_i \\
1
\end{bmatrix} =
\begin{bmatrix}
f_x & 0 & 0 \\
0 & f_y & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
X_c \\
Y_c \\
1 \\
\end{bmatrix}
$$

3.2 Image to Pixel

Pixel coordinates of an image are discrete values. In order to compute pixel coordinates ($(u, v)$), we need to express the focal length in pixel units.

$$
F_x = \frac{f_x(mm)}{s_x}, F_y = \frac{f_y(mm)}{s_y}
$$

Where $s_x$ and $s_y$ are pixel sizes(mm/pixels). $s_x$ and $s_y$ can be obtained easily if we have the the actual sensor size(mm) and image height/width.

$$
s_x = \frac{sensor\ width(mm)}{image\ width(pixels)}, s_y = \frac{sensor\ height(mm)}{image\ height(pixels)}
$$

Since pixel coordinate has its origin at top-left corner(image coordinate is centered), we need to apply a 2D translation.

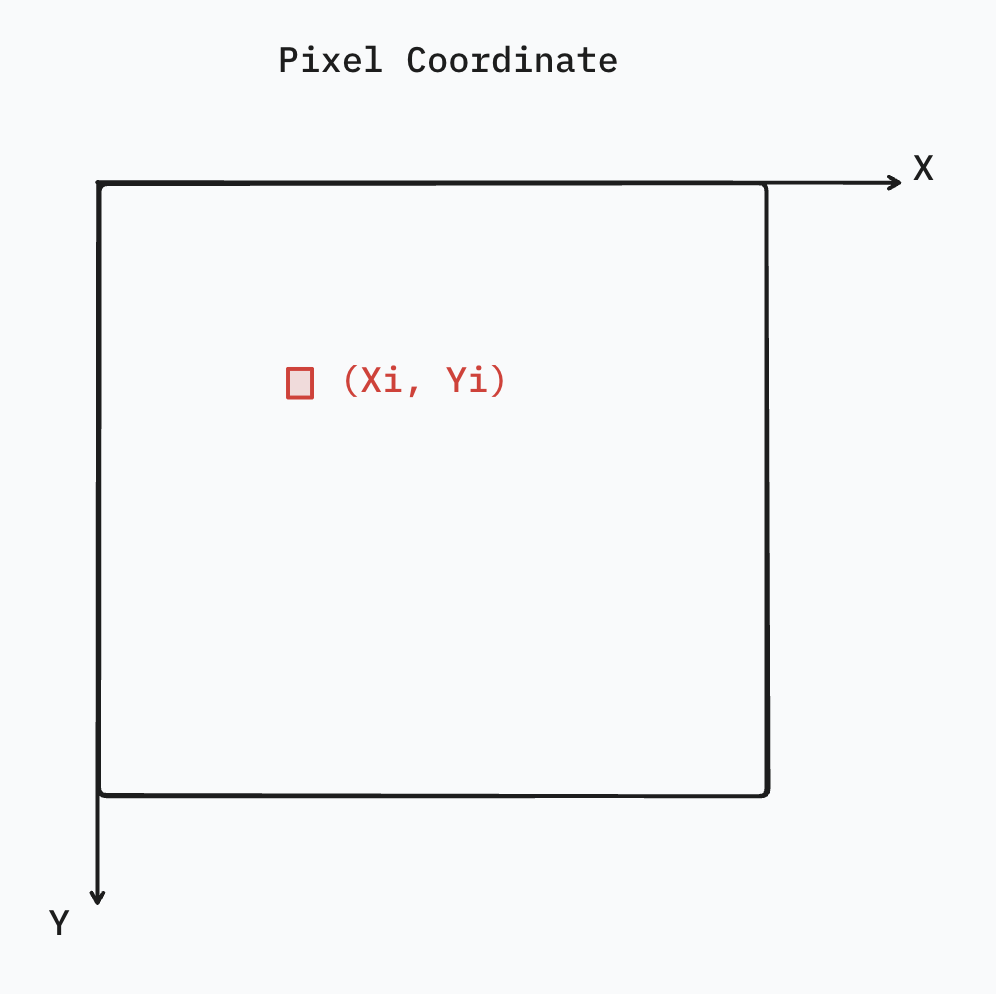
If we let the image center pixel position be $(c_x, c_y)$, from image to pixel, we can have:

$$
\begin{bmatrix}
u \\
v \\
\end{bmatrix} =
\begin{bmatrix}
\frac{1}{s_x} & c_x \\
\frac{1}{s_y} & c_y \\
\end{bmatrix}
\begin{bmatrix}
X_i \\
Y_i \\
\end{bmatrix}
$$

3.3 Camera to Pixel

Having the camera to image and image to pixel transformations, we can now have the transformation from Camera to Pixel:

$$
\begin{align}
\begin{bmatrix}
u \\
v \\
1
\end{bmatrix} &=
\begin{bmatrix}
\frac{f_x}{s_x} & 0 & c_x \\
0 & \frac{f_y}{s_y} & c_y \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
X_c \\
Y_c \\
1 \\
\end{bmatrix} \\
&=
\begin{bmatrix}
F_x & 0 & c_x \\
0 & F_y & c_y \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
X_c \\
Y_c \\
1 \\
\end{bmatrix}
\end{align}
$$

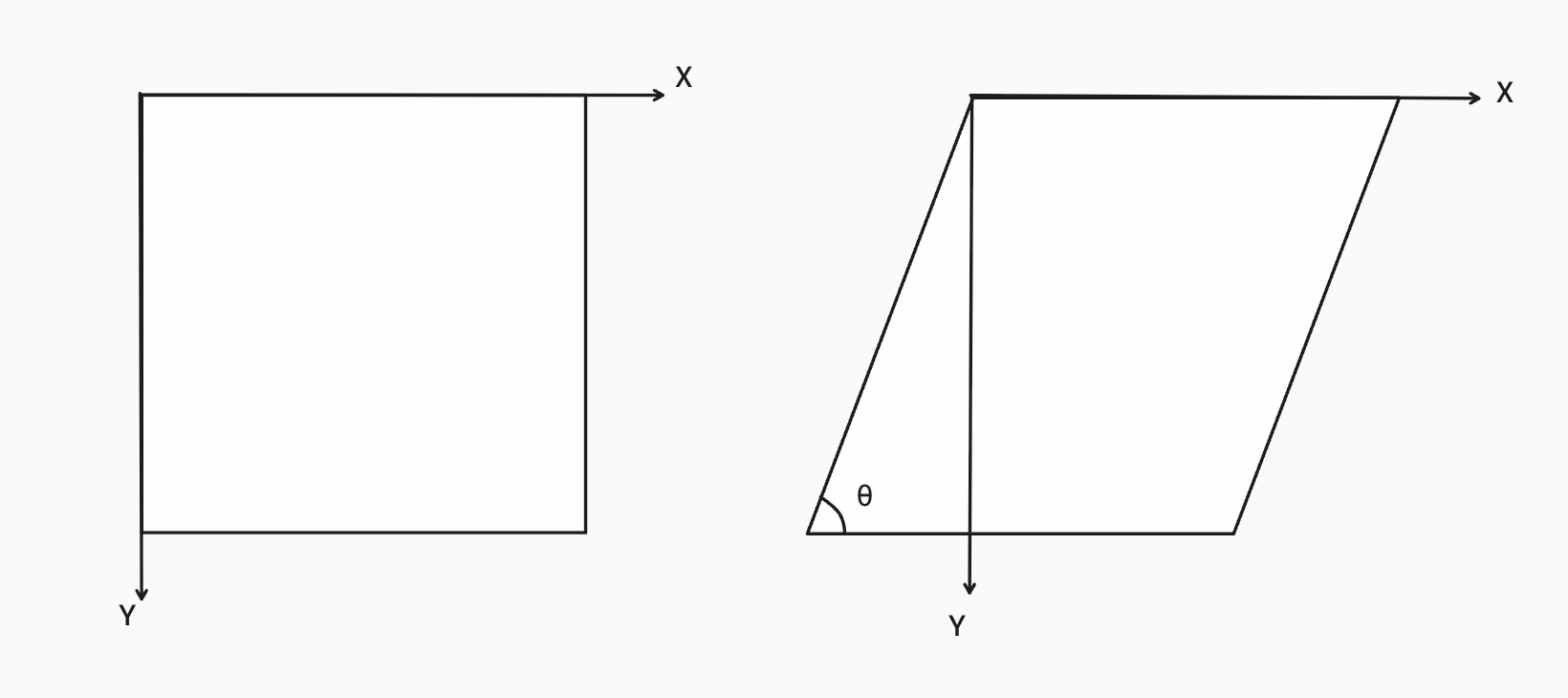
Sometimes, the image plane is not a perfect rectangle, and it is slighlt skewed. In such case, we need to apply another shear transformation to conver to the skewed plane. This transformation can be achieved by adding another parameter $s$ to the matrix.

$$
\begin{align}
\begin{bmatrix}
u \\
v \\
1
\end{bmatrix}
&=
\begin{bmatrix}
F_x & s & c_x \\
0 & F_y & c_y \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
X_c \\
Y_c \\
1 \\
\end{bmatrix}
\end{align}
$$

4. Conclusion

The overall transformation can be represented as:

$$
\begin{aligned}
\begin{bmatrix} u \\ v \\ 1 \end{bmatrix}
&=
\underbrace{
\begin{bmatrix}
F_x & 0 & c_x \\
0 & F_y & c_y \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
R & t
\end{bmatrix}
}_{\text{Camera Intrinsic + Camera Extrinsics }}
\begin{bmatrix}
X_w \\ Y_w \\ Z_w \\ 1
\end{bmatrix}
\end{aligned}
$$